The complete document is divided into five sections:
Recall that because triangles in the hyperbolic plane have angle sum less than PI, it follows that the measure of the angle at a vertex of a regular p-gon in the hyperbolic plane is less than PI-(2*PI/p). Since the angles at any vertex of a tiling sum to PI, this means that (after some algebraic simplification):
Lemma 1: In the hyperbolic plane, p_1.p_2 . . . p_q is a semi-regular tiling only if 1/ p_1 + 1/ p_2 + . . . + 1/ p_q < (q - 2)/2.
Remark 1. It is always possible to construct a sequence of polygons about a single vertex O in the hyperbolic plane if the polygons satisfy Lemma 1. The question is whether the tiling can be extended beyond a single patch to cover the entire plane. Here questions of parity arise. (See the Parity Lemma, for example, in section 3. General Theorems.) Note, also, that if adjacent centers of these polygons are connected, a q-gon is formed with angles 2*PI/p_1, 2*PI/ p_2, . . . , 2*PI/ p_q and that this q-gon has an incenter at the original vertex O.
Theorem 6 (Hyperbolic Regular Tilings). There are regular tilings of the hyperbolic plane of vertex type p^q for all positive integers p and q such that 1/p + 1/q < 1/2.
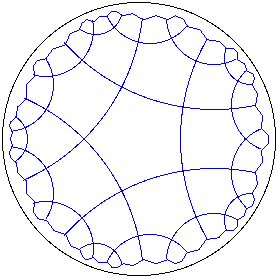
An example of a regular 5^4 tiling of the hyperbolic plane.
The proof of Threorem 6 rests on the following well-known result.
Theorem 7 (Hyperbolic Triangle Lemma). Let T be any hyperbolic triangle with angles PI/p, PI/q, and PI/r, where 1/p + 1/q + 1/r <1. Let P, Q, and R be the reflections in the sides of triangle T opposite to the angles PI/p, PI/q, and PI/r, respectively. Then the images of triangle T under the action of the distinct elements of the group of symmetries <P,Q,R> tile the hyperbolic plane.
Discussion:
An elementary proof of the fact that the images of triangle T tile the
hyperbolic plane is given in [Ca, Chapter 3]. An elementary proof that the
reflections P, Q,and R generate the entire set of symmetries for this triangle
tiling and that defining relations among the generators are: P^2 = Q^2 = R^2 =
1 and (PQ)^r = (QR)^p = (RP)^q = 1 may be found in [Mag, Chapter 2].
The figure shows a tiling by triangles with angles PI/5, PI/4, and PI/2 which can be
used to produce the 5^4 tiling above.
Proof of Theorem 6: If we let r = 1/ 2 in the preceding lemma, then for any positive integers p and q such that 1/ p + 1/ q < 1/2 , there is a tiling of the hyperbolic plane by triangles with angles PI/p, PI/q, and PI/2. Now erase all of the images of the edge of triangle T opposite to the angle with measure PI/q.
The result is a tiling of the hyperbolic plane by isosceles triangles with summit angle 2*PI/p and base angle PI/q. Next erase all the legs of the isosceles triangles which leaves a tiling of the hyperbolic plane of type p^q.
Recall that the valence of a vertex of a tiling is the number of edges (which is the same as the number of tiles) at the vertex. For small valences, the semi-regular tilings of the hyperbolic plane are easily constructed.
Theorem 8 (3-Valent Tilings). The vertex types of the 3-valent regular and semi-regular tilings of the hyperbolic plane are:
Taking q = 3 in Theorem 6 gives the existence of regular tilings of the form p^3, where p >= 7, proving part (1). Taking q odd in part 2 of Theorem 4 proves the existence of the dihedral tilings 2p.2p.q, part (2). To prove part (3), use the Hyperbolic Triangle Lemma to obtain a tiling by triangles with angles with angles PI/p, PI/q, and PI/r. Since all triangles have incenters, now use the Incenter Process, to obtain a 2p.2q.2r.
Again from the Parity Lemma and Lemma 1 above, it follows that:
Remark 2. The only possible vertex types p.q.r.s of 4-valent regular and semi-regular tilings of the hyperbolic plane are those where 1/p + 1/q +1/r +1/s < 1 and either:
From Remark 1 above, there exists a quadrilateral whose angles are 2*PI/p, 2*PI/q, 2*PI/r, and 2*PI/s which has an incenter. Since each of p, q, r, and s are even, these angles can be written as PI/j, PI/k, PI/l, and PI/m for integers j, k, l, and m. According to [C-M, p. 55]: Any n-gon with angles PI/p_1, PI/p_2, . . . , PI/p_k tiles the plane by reflection in its sides. Now use the Incenter Process to obtain part (2).
The existence of the tilings in (3) follows in a similar fashion. Note that 1/p + 1/2q +1/2s < 1/2 because 1/p + 1/q +1/r +1/s < 1 and p =r here. So the Hyperbolic Triangle Lemma implies there is a tiling by triangles with angles PI/p, PI/2q, and PI/2s. Erasing the edge opposite the angle PI/p produces a tiling by kites whose angles are PI/p, PI/q, PI/r, and PI/s. Such a kite has an incenter (at the intersection of the angle bisectors). So now the Incenter Theorem gives the result.
The tilings in (4) follow directly from part (4) of Theorem 4.
The tilings in (5) present the only difficulty. If p is even (and so q is odd), then the same proof used in (3) works. But when p is odd, this method fails. Note that a similar result appears in [G-S 1979, p. 197, Theorem 4.7.12] which claims that if p <> +/- 1 mod 6, there is at least a homeohedral tiling, though there is no claim for a hyperbolic tiling of this type.
Additional results are possible. For example,
Proof: Part (1) follows directly from Theorem 4, parts (5,6). Part (2) is proven with an argument of the same type used in (2) in Remark 2 above.
To prove part (3) begin by using the Hyperbolic Triangle Lemma to construct a tiling by triangles with angles PI/p, PI/q, and PI/k. The vertices of the p.q.p.q. . .p.q tiling consist of all the vertices of the triangle tiling at the angles whose measure is PI/k. One way to see this is to erase all the edges of the triangles coming from these vertices. That leaves an equilateral tiling by 2k-gons with alternating vertex angles 2*PI/p and 2*PI/q and the vertex at angle PI/k is an incenter for these 2k-gons. Moreover, the reflections across the edges of these 2k-gons are symmetries for the tiling, since they were symmetries of the original triangle tiling. Thus the Incenter Theorem applies and yields the result. (Note that the condition 1/p + 1/q +1/k < 1 is equivalent to the necessary condition for k/p + k/q < k-1 = (2k-2)/2 for the p.q.p.q. . .p.q tiling.)
To prove (4) begin by using Remark 1 to construct a (k+1)-gon with an incenter O that has k angles of 2*PI/p at vertices A_i (1 <= i <= k) and an angle of 2*PI/q at B.
Case 1: k is odd. Then the vertex B and the incenter O are collinear with A_(k+1)/2. The segment from A_(k+1)/2 to B creates two congruent (k+3)/2-gons with (k-1)/2 angles of 2*PI/p, an angle of PI/p at A_(k+1)/2, and an angle of PI/q at B. Since p is even, as in the discussion of Remark 2, part (2), this (k+3)/2-gon tiles the plane via reflections in its edges. Erasing the edge from A_(k+1)/2 to B and its reflections creates a tiling by the original (k+1)-gon via reflections in its edges. The Incenter Process applies to give the result.
Case 2: k is even. Then the vertex B and the incenter O are collinear with the midpoint M of the edge A_k/2 to A_(1 + k/2). The segment BM divides the (k+1)-gon into two congruent (2 + k/2)-gons with k/2 angles of 2*PI/p, an angle of PI/2 at M, and an angle of PI/q at B. As in Case 1, the (2 + k/2)-gons tile by reflection. Erasing the edge BM proceeds as in Case 1.
The proof Case 2 is easily adapted to the more general case in (4).
The proof of (5) is very similar to (4). Begin by using Remark 1 to construct a (2k+2)-gon with an incenter O that has 2 angles of 2*PI/p_i at vertices A_i and C_i (1 <= i <= k), an angle of 2*PI/q at B, and an angle of 2*PI/r at D. Connect B and D to create two congruent (k+2)-gons which tile the plane by reflection (this is where the evenness of p_i is used). Now erase segment BD and its reflections to form a tiling by (2k+2)-gons and apply the Incenter Process.
Examples of vertex types from Theorem 9: