Plane Tiling: A plane tiling is a countable family of polygons T_1, T_2, .
. . called tiles such that their union is the entire plane and
the interiors of the tiles are pairwise disjoint. The complete document is divided into five sections:
Plane Tiling: A plane tiling is a countable family of polygons T_1, T_2, .
. . called tiles such that their union is the entire plane and
the interiors of the tiles are pairwise disjoint.
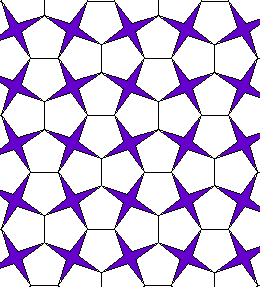
Edge-To-Edge Tiling: Throughout we assume that our tilings are edge-to-edge, that is, the corners and sides of the polygonal tiles form all the vertices and edges of the tiling and vice versa.
This figure shows an edge-to-edge tiling of the plane by regular pentagons and
four-pointed stars.
Much of our attention will focus on the very special type of "regular'' tiles
that were informally described in the Historical Background
section and which have been of interest historically.
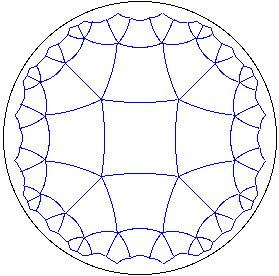
Regular Tiling: An edge-to-edge tiling is said to be regular if all the polygons are congruent to a single regular polygon.
This figure shows the central section of the regular tiling of the hyperbolic
plane by quadrilaterals five at each vertex. This tiling is denoted by 4^5. The
notational convention is explained below.
Vertex Type: A vertex of a tiling is said to be of type p_1.p_2 . . . p_q if the polygons about this vertex in cyclic order are a p_1-gon, a p_2-gon, . . . , and a p_q-gon. Reversing the cyclic order of the tiles about a vertex is not distinguished as a different type.
Archimedean Tiling: An edge-to-edge tiling is Archimedean if (1) each
tile is a regular polygon (not all congruent) and (2) all vertices are the same
type.
Often we impose additional symmetry conditions on Archimedean tilings.
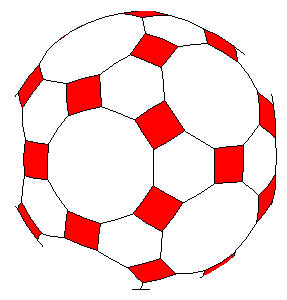
Semi-Regular Tiling: An Archimedean tiling whose symmetries are transitive on its vertices is called semi-regular. That is, given any two vertices of the tiling, there is some symmetry which maps one vertex to the other. Such tilings are also called uniform.
The figure shows a semi-regular 4.6.10 tiling of the sphere.
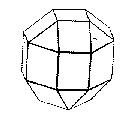There is some confusion about the language here. One reason is that for
Euclidean tilings, there is no difference between the Archimedean and the
semi-regular tilings. For spherical tilings, there is single vertex type,
3.4.4.4, which occurs in an Archimedean form that is not semi-regular and in a
form which is semi-regular. According to [F-T] the
3.4.4.5 Archimedean tiling
(seen to the right) was discovered by Miller in 1930. I
This Archimedean 3.4.4.4 tiling arises by modifying the semi-regular
3.4.4.4 tiling of the sphere (see the figure to the right) which we saw in Kepler's set of
figures from his 1619 text Harmonices Mundi
illustrated on the previous page.
Notice that the semi-regular tiling has three bands of squares,
one at the "equator" and two through the
"poles." On each side of these bands of squares are other bands of tiles that consist of alternating
triangles and squares. Simply rotate one such band one unit relative to adjacent band of squares.
to arrive at the the Archimedean 3.4.4.4 tiling. Notice that now there is only one band of
squares (see figure above) instead of three, and thus the symmetry is broken.
However, in the hyperbolic plane there are an infinite
number of Archimedean tilings which are semi-regular. An entire class of them,
the 4.4.4.q (q >= 5) tilings can be drawn with my program. I have not seen
these figures elsewhere in the literature, but authors occasionally make
reference to their existence.
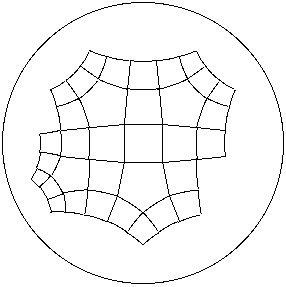
The figure to the right shows an Archimedean, but not semi-regular 4^3.5 tiling
of the hyperbolic plane.
Valence: The valence of a vertex in a tiling is the number of edges (which is the same as the number of tiles) at the vertex. In a regular, semi-regular, or an Archimedean tiling, the valence is constant over all vertices.