Constructing Semi-Regular Tilings
The following document is based on a talk given at the Spring 1995 Meeting of
the Seaway Section of the Mathematical Association of America. The meeting was held at
Hobart and William Smith Collleges in Geneva,
New York on April 21--22, 1995.
This document is divided into five sections:
- Introduction and Historical Background
- Notation and Definitions
- General Theorems
- Hyperbolic Results
- References
The five familiar regular or Platonic polyhedra were well-known in antiquity.
A toy regular dodecahedron was found in Padua in Etruscan ruins dating from 500
B.C. See [Mar,199]. Theatetus (419--369 B.C.)
is given the credit for having
developed the abstract notion of a regular polyhedra. Somewhat less familiar
are the semi-regular polyhedra (whose faces are regular polygons of two or more
different types arranged similarly about each vertex) that were also known to
the Greeks. Because they were described in Archimedes' writings, they are often
called Archimedean polyhedra. There are thirteen such polyhedra as well as two
infinite classes which are often referred to as regular prisms and antiprisms.
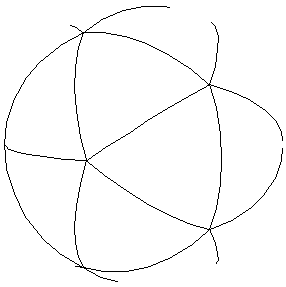 A sphere that passes through all the vertices may be circumscribed about any of
the regular or semi-regular polyhedra. If the polyhedron is then projected onto
the sphere from its center, a tiling of the sphere by regular (spherical)
polygons is obtained. Conversely, a tiling of the sphere by regular polygons
(of three or more sides, three or more at a vertex) similarly arranged about
each vertex can be used to produce one of the polyhedra mentioned above by
connecting adjacent vertices with straight line segments. In this way we can
think of the regular and semi-regular polyhedra as solving a very special
tiling problem on the sphere. For
example, the icosahedron is a regular tiling of the sphere using five triangles at
avertex.
A sphere that passes through all the vertices may be circumscribed about any of
the regular or semi-regular polyhedra. If the polyhedron is then projected onto
the sphere from its center, a tiling of the sphere by regular (spherical)
polygons is obtained. Conversely, a tiling of the sphere by regular polygons
(of three or more sides, three or more at a vertex) similarly arranged about
each vertex can be used to produce one of the polyhedra mentioned above by
connecting adjacent vertices with straight line segments. In this way we can
think of the regular and semi-regular polyhedra as solving a very special
tiling problem on the sphere. For
example, the icosahedron is a regular tiling of the sphere using five triangles at
avertex.
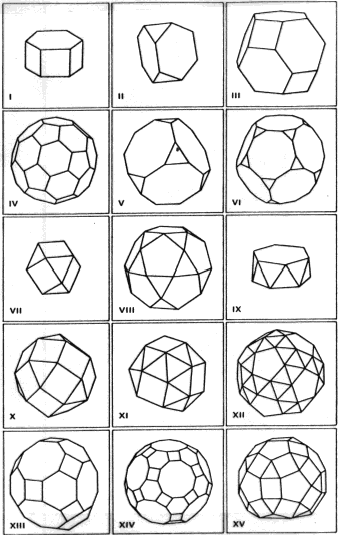
Though regular and semi-regular polyhedra were known in antiquity, this work
seems to have been lost and the results were only gradually rediscovered during
the Renaissance. Artists such as Albrect Durer and Pierro della Francesca made
drawings of many of the semi-regular polyhedra. Johannes Kepler was the first
person of this period to give a
complete description of such figures in his Harmonices Mundi which
appeared in 1619. The figure below gives examples of all of the classes of
semi-regular tilings of the sphere.
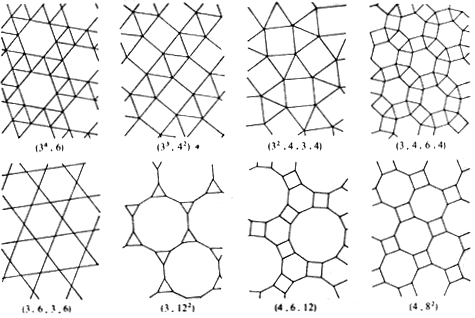
In the Euclidean plane, tilings using only regular polygonal tiles were known
and used in antiquity, but were not completely and systematically classified.
It was Kepler, again, who generalized the idea of the Archimedean polyhedra and
found all eleven so-called Archimedean tilings of the Euclidean plane. These
tilings employ one or more types of regular polygon similarly arranged about
each vertex. These eight tilings employing polygons of more than one type appear
in the figure below.
Surprisingly, Kepler's work on Euclidean plane tilings seems to
have been forgotten for the better part
of 300 years. Grunbaum and Shephard claim that the first correct
determination of the eleven Archimedean Euclidean tilings in modern times was
by Robin in 1887, Sommerville in 1905, and then Andreini in 1907. Apparently
they were aware neither of Kepler's work nor each others'. In fact, as late as
1931, certain authors appeared to be unaware of such work. Grunbaum and
Shephard further claim that many other authors of this period gave defective
treatments of this problem failing to
list one or another of the types of Archimedean tilings.
[G-S 1987 or G-S 1989,
Chapter 2.10]
The nineteenth century creation of hyperbolic geometry provides
another arena for creating tilings. The hyperbolic plane is amenable to an
infinite number of different tilings by regular polygons. It is well-known that
regular hyperbolic p-gons appearing q at a vertex will tile the hyperbolic
plane whenever 1/ p + 1/q < 1/2. Such tilings are important because when p =
q = 4n they are the universal covering spaces of orientable compact Riemann
surfaces ([C-M, Chapter 5],
[H-CV, Section 49]) and because of their intimate
relation to modular groups and automorphic functions
([K-F], [L]). Drawings of
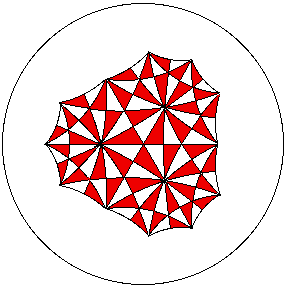
such tilings, especially those employing the Poincare model, are aesthetically
appealing. Pictures of such tilings, for example septagons (divided into
fourteen alternating black-and-white right triangles) meeting three at a vertex
appear in the mathematical literature as early as 1890
[K-F, Figure 33]. A
similar illustration of triangulated regular hyperbolic hexagons meeting four at
vertex (see the cover of [G]) was the inspiration for
M. C. Escher's series of four
woodcuts "Circle Limit I--IV" [Co, Figure 1],
[D1, Figure 1]. The figure below shows a tiling by septagons
three at a vertex, divided into alternating red and white triangles.
The general problem of tiling the hyperbolic plane with two or more different
regular polygons similarly arranged about each vertex seems to have attracted
less attention. In fact, the author was able to locate only a single such
illustration [R, Figure 11] which shows a
tiling of the
hyperbolic plane using two regular octagons and a single hexagon at each
vertex.
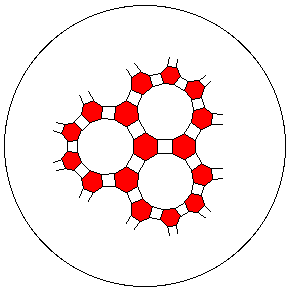
This figure shows a tiling of the hyperbolic plane using three regular poylgons at a
vertex: a quadrilateral, an hexagon, and a 14-gon.
For an introduction to the terminology and defintions used to describe regular and
semi-regular tilings, see 2. Notation and Definitions.
Sections 3. General Theorems and 4.
Hyperbolic Results describe some
relatively simple geometric processes that allow one to
construct several such tilings. For additional sources of material, see the
References section.
Author: Kevin Mitchell (mitchell@hws.edu)
Last Update: 13 February 1996.
 A sphere that passes through all the vertices may be circumscribed about any of
the regular or semi-regular polyhedra. If the polyhedron is then projected onto
the sphere from its center, a tiling of the sphere by regular (spherical)
polygons is obtained. Conversely, a tiling of the sphere by regular polygons
(of three or more sides, three or more at a vertex) similarly arranged about
each vertex can be used to produce one of the polyhedra mentioned above by
connecting adjacent vertices with straight line segments. In this way we can
think of the regular and semi-regular polyhedra as solving a very special
tiling problem on the sphere. For
example, the icosahedron is a regular tiling of the sphere using five triangles at
avertex.
A sphere that passes through all the vertices may be circumscribed about any of
the regular or semi-regular polyhedra. If the polyhedron is then projected onto
the sphere from its center, a tiling of the sphere by regular (spherical)
polygons is obtained. Conversely, a tiling of the sphere by regular polygons
(of three or more sides, three or more at a vertex) similarly arranged about
each vertex can be used to produce one of the polyhedra mentioned above by
connecting adjacent vertices with straight line segments. In this way we can
think of the regular and semi-regular polyhedra as solving a very special
tiling problem on the sphere. For
example, the icosahedron is a regular tiling of the sphere using five triangles at
avertex.



