The complete document is divided into five sections:
Theorem 1 (Regular Tilings). There is a regular tiling of type p^q for all p, q >= 3. In particular,
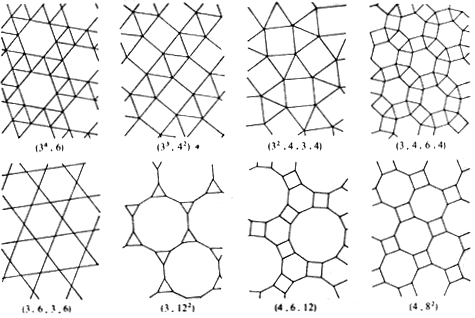
Theorem 2 (Kepler). There are 8 semi-regular tilings of the Euclidean plane: 3.12^2, 4.6.12, 4.8^2, 3.4.6.4, 3.6.3.6, 3^4.6, 3^3.4^2, and 3^2.4.3.4.

Discussion of Theorems 2 and 3: To construct the semi-regular tilings, the typical method is to proceed in two steps:
The elimination process, uses the fact that the measure of a vertex angle of a regular p-gon is
Because the angles at any vertex of a tiling sum to 2*Pi, p_1.p_2 . . . p_q is a semi-regular tiling only if (after a bit of simplification)
In addition to the vertex types given by Kepler, the following types satisfy the first equation above but cannot be extended beyond a small patch of tiles to give a full tiling of the Euclidean plane: 3.7.42, 3.8.24, 3.9.18, 3.10.15, 4.5.20, 5^2.10, 3^2.6^2, 3^2.4.12, 3.4.3.12, and 3.4^2.6.
Similarly the following vertex types satisfy the second equation above but do not lead to tilings of the sphere: 3^2.n (n > 3), 5^2.n (n = 3,4,6,7,8,9), 3.7^2, 3.9^2, 3^2.4.n (4 <= n <=11), 3^2.5.n (5 <= n <= 7), 3.4^2.5, 3.4.3.n (5 <= n <=11), 3.5.3.n (n = 6,7).
Lemma 1 (Parity Lemma). Let T be a semi-regular tiling.
A check shows that (1) eliminates all the potential vertex types listed above with the exception of 3^2.4.12 which is eliminated by (2).
For further parity results relating to vertex types of semi-regular tilings, see [Z] or [W].
Theorem 4 is, itself, a consequence of a much more general result.
Theorem 5 (The Incenter Process). Given a (possibly non-regular) q-gon such that:
Proof: The first condition implies that all the angles at a single vertex are reflections of each other. If p_i tiles meet at the i-th vertex, then the angle between consecutive edges there is 2*Pi/p_i, where 1 <= i <= q.
 If we connect the incenters of the adjacent polygons about the i-th vertex, a
p_i-gon is formed. Every edge of this p_i-gon is composed of two collinear
congruent radii of the incircles of adjacent q-gons. So the p_i-gon is
equilateral. Since the vertex angles of the p_i-gon are also congruent (being
reflected one into the next across adjacent edges of the q-gon) the p_i-gon is
actually regular. Thus, at each incenter of the original tiling we have
constructed a sequence of regular polygons p_1.p_2 . . . p_q. The sequence is
the same at every incenter, since adjacent in q-gons are reflected onto each
other across shared edges. So we have constructed the desired tiling.
If we connect the incenters of the adjacent polygons about the i-th vertex, a
p_i-gon is formed. Every edge of this p_i-gon is composed of two collinear
congruent radii of the incircles of adjacent q-gons. So the p_i-gon is
equilateral. Since the vertex angles of the p_i-gon are also congruent (being
reflected one into the next across adjacent edges of the q-gon) the p_i-gon is
actually regular. Thus, at each incenter of the original tiling we have
constructed a sequence of regular polygons p_1.p_2 . . . p_q. The sequence is
the same at every incenter, since adjacent in q-gons are reflected onto each
other across shared edges. So we have constructed the desired tiling.
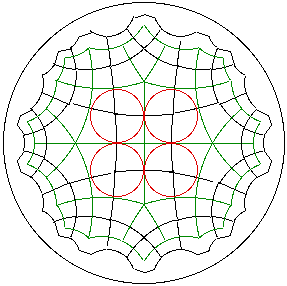
Example. A reflection tiling (green) of the hyperbolic plane using 'kites' with angles Pi/6, Pi/2, 2*Pi/5, and Pi/2. These kites have circles inscribed in them (red). The centers of these circles are the vertices of a semi-regular 6.4.5.4 tiling (black).
Proof of Theorem 4:
 1. Existence of the Dual q^p.
1. Existence of the Dual q^p.
Since a regular p-gon has an incenter and since there are q tiles at all p
vertices of the p-gon, the p^q tiling satisfies the hypotheses of Theorem 5.
This proves that the dual regular tiling q^p exists.
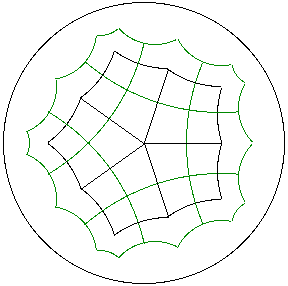
Example. The regular 5^4 tiling of the hyperbolic plane in black and its dual regular tiling p^q = 4^5 in green. The vertices of the dual tiling lie at the center of the original 5-gons.
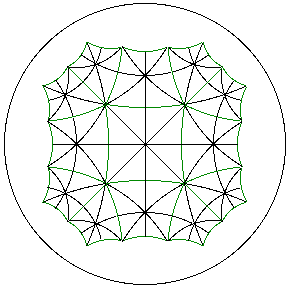 2. Existence of p.2q.2q.
2. Existence of p.2q.2q.
Divide each tile of p^q into p congruent isosceles triangles by connecting
the center of the p-gon to each of its vertices. Since every
triangle has an incenter, this produces a triangle tiling of the plane. Since
reflections across all edges of these triangles are, in fact,
symmetries of the original p^q,
they are also symmetries of the triangle tiling. Thus, the triangle tiling
satisfies the conditions of Theorem 5. Since the summit angle of the triangle
(at the center of the p-gon) is 2*Pi/p and the base angles are Pi/q =
2*Pi/2q, we obtain a p.2q.2q. Applying this result to the dual q^p tiling
produces a 2p.2p.q.
Example.
A triangulation, in black, of the p^q = 4^5 tiling, in green,
of the hyperbolic plane. The isosceles
triangles have angles Pi/4, Pi/4, and Pi/5. Note that all triangles have incenters.
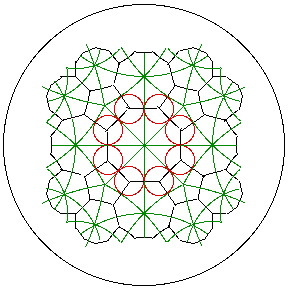 The triangles, now in green, have inscirbed circles, here in red. Connecting centers
of these circles produces the 2p.2p.q = 8.8.5 semi-regular tiling of the hyperbolic
plane, in black. Note that the triangles are reflected one into the other across
their edges and that all of these reflections are symmetries of the original 4^5.
The triangles, now in green, have inscirbed circles, here in red. Connecting centers
of these circles produces the 2p.2p.q = 8.8.5 semi-regular tiling of the hyperbolic
plane, in black. Note that the triangles are reflected one into the other across
their edges and that all of these reflections are symmetries of the original 4^5.
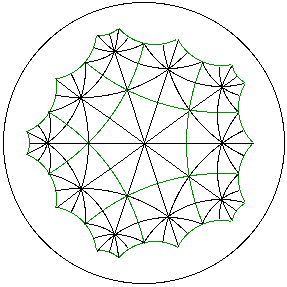 3. Existence of 4.2p.2q.
3. Existence of 4.2p.2q.
Subdivide each p-gon of the original tiling into 2p triangles by connecting the
center of the p-gon to each of its vertices and to the midpoint of each of its
edges. The triangles within a p-gon are transformed successively
into each other by reflections across the edges emanating from the center of the
p-gon. Using reflections across the original edges of the p-gon allows us to transform
the triangles of any one p-gon into any other. Thus the conditions of
Theorem 5 are satisfied. Since the angles of the triangle are Pi/2, Pi/p, and Pi/q, we
obtain a 4.2p.2q.
Example. Starting with the p^q = 5^4 tiling of the hyperbolic plane, in green, we form a triangulation, consisting of all the black and green edges, by right triangles with angles Pi/2, Pi/5, and Pi/4. The vertices of triangles are the centers and vertices of the original p-gons as well as the midpoints of each of the edges.
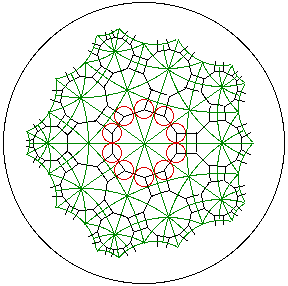 But all triangles, now in green, have inscirbed circles (in red). Connecting centers
of these circles produces the 4.2p.2q = 4.10.8 semi-regular tiling of the hyperbolic
plane, here in black.
But all triangles, now in green, have inscirbed circles (in red). Connecting centers
of these circles produces the 4.2p.2q = 4.10.8 semi-regular tiling of the hyperbolic
plane, here in black.
 4. Existence of p.q.p.q.
4. Existence of p.q.p.q.
Form a tiling by rhombi by using only the segments from the centers of the p^q to the
vertices of the p^q. Adjacent rhombi are
reflections of each other across edges they share. Each rhombus has an incenter
at the intersection
of its diagonals. Since the angles of the rhombus are alternately 2*Pi/p and
2*Pi/q, we obtain a p.q.p.q.
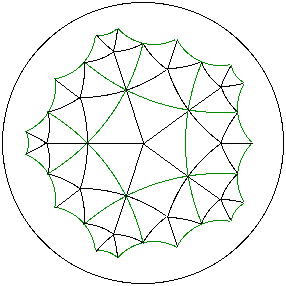
Example. The green p^q = 5^4 tiling of the hyperbolic plane and its associated tiling by rhombii. Each rhombus has angles 2*Pi/5, Pi/2, 2*Pi/5, and Pi/2).
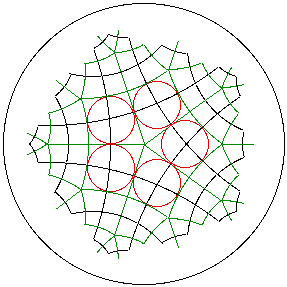 Every green rhombus has an incircle (red) with center at the intersection of its
diagonals. Connecting these centers
produces the p.q.p.q = 5.4.5.4 semi-regular tiling (black) of the hyperbolic plane.
Every green rhombus has an incircle (red) with center at the intersection of its
diagonals. Connecting these centers
produces the p.q.p.q = 5.4.5.4 semi-regular tiling (black) of the hyperbolic plane.
 5. Existence of 4.p.4.q.
5. Existence of 4.p.4.q.
If we overlay the dual q^p tiling on the p^q tiling, a tiling by
kites with angles PI/2, 2*PI/p, PI/2, and 2*PI/q is created.
Each kite has an incenter (at the
intersection of its four angle bisectors) and so we obtain a 4.p.4.q.
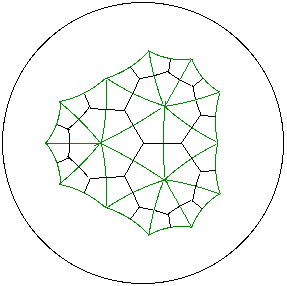
Example. A p^q = 3^7 regular tiling, in green, of the hyperbolic plane with its dual q^p = 7^3 tiling, in black. Together these tilings form 'kites' with with angles Pi/2, 2*Pi/3, Pi/2 and 2*pi/7.
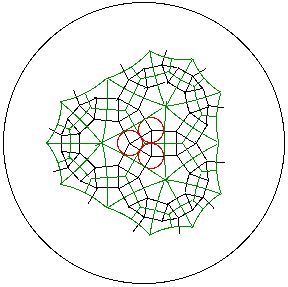 Every kite (in green) has an incircle (red) with center at the intersection of its
angle bisectors. Connecting these centers
creates the 4.p.4.q = 4.3.4.7 semi-regular tiling (black) of the hyperbolic plane.
Every kite (in green) has an incircle (red) with center at the intersection of its
angle bisectors. Connecting these centers
creates the 4.p.4.q = 4.3.4.7 semi-regular tiling (black) of the hyperbolic plane.
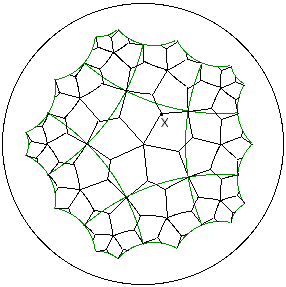 6. Existence of 3.3.p.3.q.
6. Existence of 3.3.p.3.q.
Form irregular pentagons with angle 2*PI/p at the center of the p-gon,
2*PI/3 at the 'appropriate' interior point X
of the p^q, 2*PI/q at a vertex
of the p^q, and then consecutive angles of 2*PI/3 at
the image of X under a rotation of
2*PI/q about the vertex and the image of X under a rotation of
-2*PI/p about the center. Note: These pentagons are not reflected
into each other across their shared edges. Rather, the rotations of 2*Pi/p about the
center of each p-gon of the original p^q and the rotations of 2*p/q about each
vertex of the p-gons are symmetries of this pentagonal tiling.
Thus, the pentagonal tiling is 'sufficiently symmetric' for a modified version of
Theorem 5 to apply.
Example. A tiling by irregular pentagons (in black) with angles 2*Pi/3, 2*Pi/3, 2*Pi/5, 2*Pi/3, Pi/2, and 2*Pi/3. Rotational symmetries of the underlying p^q = 5^4 regular tiling (green) are used to tile the plane with these pentagons.
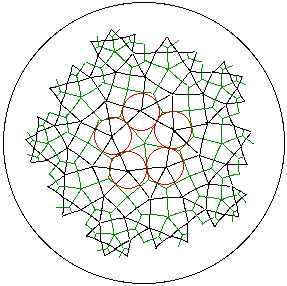 Each pentagon (in green) has an incircle (in red). Connecting centers of these
creates the 3^2.p.3.q = 3^2.5.3.4 semi-regular tiling of the hyperbolic plane, here
in black.
Each pentagon (in green) has an incircle (in red). Connecting centers of these
creates the 3^2.p.3.q = 3^2.5.3.4 semi-regular tiling of the hyperbolic plane, here
in black.
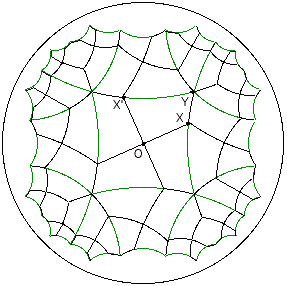 7. Existence of 3.p.3.p.3.q/2.
7. Existence of 3.p.3.p.3.q/2.
Form irregular hexagons using a vertex Y of the p^q, an appropriate point X
on an edge of the p^q containing Y, the center of the p-gon O, the
image X' of X under a rotation of 2*PI/p about O. The remainder of the
hexagon is obtained by reflecting across the edge containing Y and X'.
Symmetries of this hexagonal tiling include rotations of 2*Pi/p about the centers
of the original p-gons and reflections across the edges of the p-gons. The proof
of Theorem 5 can be adapted to this situation.
Example.
A tiling by irregular hexagons (in black) with angles
2*Pi/3, Pi/3, 2*Pi/3, Pi/2, 2*Pi/3, and 2*Pi/5 based on the underlying
p^q = 4^6 tiling (in green) of the hyperbolic plane. The hexagon tiling can be
rotated about the center of any 4-gon and reflected across the edge of any
4-gon.
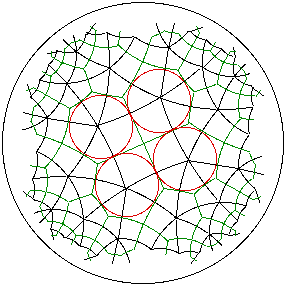
Each hexagon (in green) has an incircle (red). Connecting centers of these
creates the 3.p.3.p.3.q/2 = 3.4.3.4.3.3 semi-regular tiling of
the hyperbolic plane, here in black.
Using Theorem 4 and the existence of the regular tilings of the Euclidean plane and the sphere in Theorem 1, we obtain most of the semi-regular tilings in the Euclidean plane and on the sphere listed in Theorems 2 and 3. These are shown in the table below, along with some reperesentative hyperbolic tilngs.
Regular Dual p.2q^2 4.2p.2q p.q.p.q 4.p.4.q 3^2.p.3.q 3.p.3.p.3.q/2
Euclidean 3^6 6^3 3.12^2 4.6.12 3.6.3.6 4.3.4.6 3^5.6 3^6
4^4 4^4 4.8^2 4.8^2 4^4 4^4 3^4.3.4
6^3 3^6 6^3 4.6.12 3.6.3.6 4.3.4.6 3^5.6
Sphere 3^3 3^3 3.6^2 4.6^2 3^4 3.4.3.4 3^5
3^4 4^3 3.8^2 4.6.8 3.4.3.4 3.4^3 3^4.4
3^5 5^3 3.10^2 4.6.10 3.5.3.5 3.4.5.4 3^4.5
4^3 3^4 3.8^2 4.6.8 3.4.3.4 3.4^3 3^4.4
5^3 3^5 3.10^2 4.6.10 3.5.3.5 3.4.5.4 3^4.5
Hyperbolic 3^7 7^3 3.14^2 4.6.14 3.7.3.7 3.4.7.4 3^5.7
4^5 5^4 4.10^2 4.8.10 4.5.4.5 4^3.5 3^2.4.3.5
4^6 6^4 4.12^2 4.8.12 4.6.4.6 4^3.6 3^2.4.3.6 3^3.4.3.4
5^8 8^5 5.16^2 4.10.16 5.8.5.8 4.5.4.8 3^2.5.3.8 3.4.3.5.3.5
To complete the proof of Theorems 2 and 3, note that the remaining 5-valent
semi-regular tiling in the Euclidean plane is 3^3.4^2. It is easily constructed
by hand using alternating parallel bands of equilateral triangles and squares.
Similarly, the prisms 4^2.n on the sphere are
constructed by using a band of n 4-gons capped above and below by an n-gon and
the antiprisms 3^3.n are formed by taking a band of 2*n equilateral triangles
and again capping with n-gons.Though we have not outlined how to produce the regular tilings in Theorem 1, using (1) of Theorem 4, we see that in the Euclidean plane the hexagon tiling 6^3 is dual to the triangle tiling 3^6 and on the sphere the octahedron 3^4 is dual to the cube 4^3 and the dodecahedron 5^3 is dual to the icosahedron 3^5. So we can get away with constructing the square tiling 4^4 and triangle tiling 3^6 in the Euclidean plane and the tetrahedron 3^3, cube 4^3, and icosahedron 3^5 on the sphere.