Math 360: Foundations of Geometry

Offered:     Spring 2011
Instructor:  Kevin J. Mitchell
Office: Lansing 305 
Phone:  (315) 781-3619
Fax:    (315) 781-3860
E-mail: mitchell@hws.edu

Office Hours: Monday, Wednesday, & Thursday 2:00 to 4:00, and Friday 1:30 to 2:30.
          I am often available at other times by appointment.

Class:    M-W-F 10:10AM - 11:05AM Napier Hall 202                  
Text:     Euclidean and Non-Euclidean Geometries, (Third Edition) 
          by Marvin Jay Greenberg
Optional: A Certain Ambiguity: A Mathematical Novel, by Gaurav Suri 
          and Hartosh Singh Bal. (Princeton University Press)

About the Course

This course is about geometry and, in particular, the discovery (creation) of non-Euclidean geometry about 200 years ago. At the same time, the course serves as an example of how the discipline of mathematics works, illuminating the roles of axioms, definitions, logic, and proof. In this sense, the course is about the process of doing mathematics.

The course provides a rare opportunity to see how and why mathematicians struggled with key ideas---sometimes getting things wrong, other times having great insights (though occasionally they did not recognize this fact). History is important to this subject; this course should convince you that mathematics is a very human endeavor.

The course focuses on Euclid's Parallel Axiom: "For any line l and any point P not on l, there is a unique line through P parallel to l." In particular, could this axiom be deduced as a consequence of the earlier and more intuitive axioms that Euclid had laid out for his geometry? Mathematicians struggled with this question for 2000 years before successfully answering it. The answer had a profound philosophical effect on all later mathematics, as we will see.

One of the goals of the course is to convince you that if you "believe in" Euclidean geometry (the ordinary, everyday geometry that you studied in high school), then you must also "believe in" hyperbolic geometry which is quite different from and contradictory to Euclidean geometry. For example, in hyperbolic geometry, triangles have less than 180 degrees (see the figure to the left) and there are no rectangles!

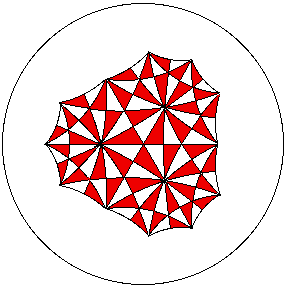
An obvious question, then, is whether the universe is actually Euclidean or hyperbolic. Note that it is not possible to "prove" that the world is Euclidean by measuring a physical triangle and showing that it has 180 degrees. Why? However, if the universe were hyperbolic, it might be possible to show this by measuring triangles. How? In fact, the great mathematician Gauss tried to do exactly this! (The figure to the left shows part of a tiling of the hyperbolic plane by congruent hyperbolic triangles. Do they look congruent?)

Here are a few of the other interesting results from the strange world of hyperbolic geometry to pique your curiosity and that you will actually prove during the term:

The course rewards careful, attentive reading and regular review of previously covered material. You need to know the definitions, axioms, and statements of previous theorems well to be able to derive new and interesting results. Be sure to read with a pencil in your hand, especially to draw figures that relate to the material being discussed.

Rough Outline of Weekly Readings

Assessment

There will be three take-home exams. The first will be assigned near mid-term (but this date may change depending on the pace at which we cover material). The second or Penultimate Assignment will be given out about 2 weeks before the end of term. It will review much of the material from the second half of the course. The third exam will be given out on the last day of class and will be due on the at the time scheduled for the final exam for this course. There will be regular homework assignments, a total of about 12 to 15 or for the entire term. As well, you will be required to give class presenations on specific homework problems.

The take-home final will cover material primarily from the last few weeks of the course and will include a careful review of hyperbolic geometry that will require a number of hyperbolic constructions. (E.g., construct an equilateral triangle with three 45 degree angles!)

Assignments are due at the beginning of class. Late assignments will incur a substantial penalty and will be rejected entirely if more than two days late. Since the course builds on each assignment, it is extremely important for you to get them done on time.

I encourage you to discuss material with each other. However, each person should write up his work individually. On the take-home exams you may not discuss the problems with anyone except me.

Together the two take-home exams and final assignments count for 50% of your final grade. The presentations and homework assignments will make up the remainder (50%, split about 15% and 35%) of your grade. I reserve the right to consider class participation (including attendance) as a factor.

Note: There may be a mini-project in conjunction with Professor Vaughn's Math 110 classes to present material related to Eratosthenes' experiment to measure the circumference of the earth. Another opportunity for a mini-project seminar presentation (around Pi Day) would be to describe Buffon's needle experiment. This is a probabilistic way to determine Pi that uses elementary calculus.

More Reading

In some years I have assigned extensive writing projects in the course. This time I expect to assign more class presentations, in part, because the end of Spring Term always seems especially hectic. Nonetheless, I thought I would present the list of readings and topics that I provide when I do require projects for the course. Any of them would be interesting for you to read.

Let me begin by mentioning a novel that I read few years ago. It is wonderfully relevant for this course. A Certain Ambiguity: A Mathematical Novel by Gaurav Suri and Hartosh Singh Bal. (Princeton University Press).

Additional Sources in the Library

I have placed the following texts On Reserve in the Library. There will be some short assigned reading in the first few weeks in some of these texts.

A Note about the Center for Teaching and Learning (CTL)

At Hobart and William Smith Colleges, we encourage students to seek the academic collaboration and resources that will enable them to do their best work. The CTL offers a variety of resources that can help students achieve academic success, including Teaching Fellows (for help in Anthropology/Sociology, Biology, Chemistry, Economics, Geoscience, Philosophy, Physics, Psychology, Spanish & Hispanic Studies), Writing Colleagues (for help on papers), Study Mentors (for help with study skills and time management), Group Study Tables (for content help in specific courses), and more. For more information on these resources, visit the CTL webpage at http://www.hws.edu/academics/ctl/index.aspx, or visit the CTL Blackboard site.

Disability Accommodations: If you are a student with a disability for which you may need accommodations, you should self-identify and register for services with the Coordinator of Disability Services at the Center for Teaching and Learning (CTL), and provide documentation of your disability. Disability related accommodations and services generally will not be provided until the registration and documentation process is complete. The guidelines for documenting disabilities can be found at the following website: http://www.hws.edu/disabilities.

Please direct questions about this process or Disability Services at HWS to David Silver, Coordinator of Disability Services, at silver@hws.edu or x3351.

Hobart and William Smith Colleges: Department of Mathematics and Computer Science
Hobart and William Smith Colleges
Department of Mathematics and Computer Science
Copyright © 2011
Author: Kevin Mitchell (mitchell@hws.edu)
Last updated: January 2011