Math 360: Foundations of Geometry

Offered:     Fall 2000
Instructor:  Kevin J. Mitchell
Office: Lansing 305 
Phone:  (315) 781-3619
Fax:    (315) 781-3860
E-mail: mitchell@hws.edu

Office Hrs:  M & W 1:30 to 2:30, T & T 10:30 to Noon. 
             Often available at other times by appointment.

Class:   M-W-F 11:15 to 12:20 in Napier 102                   
Text:    Euclidean and Non-Euclidean Geometries, (Third Edition) 
         by Marvin Jay Greenberg

Information Available:

  1. About the course
  2. Outline of Weekly Readings
  3. Assessment
  4. Office Hours
  5. Project Guidlines
  6. Additional Sources on Reserve

About the Course

This course is about geometry and, in particular, the discovery (creation) of non-Euclidean geometry less than 200 years ago. At the same time, the course serves as an example of how the discipline of mathematics works, illuminating the roles of axioms, definitions, logic, and proof. In this sense, the course is about the process of doing mathematics.

The course provides a rare opportunity to see how and why mathematicians struggled with key ideas---sometimes getting things wrong, other times having great insights (though occasionally they did not recognize this fact). History is important to this subject; this course should convince you that mathematics is a very human endeavor.

The course focuses on Euclid's Parallel Axiom: "For any line l and any point P not on l, there is a unique line through P parallel to l." In particular, could this axiom be deduced as a consequence of the earlier and more intuitive axioms that Euclid had laid out for his geometry? Mathematicians struggled with this question for 2000 years before successfully answering it. The answer had a profound philosophical effect on all later mathematics, as we will see.

One of the goals of the course is to convince you that if you "believe in" Euclidean geometry (the ordinary, everyday geometry that you studied in high school), then you must also "believe in" hyperbolic geometry which is quite different from and contradictory to Euclidean geometry. For example, in hyperbolic geometry, triangles have less than 180 degrees and there are no rectangles! An obvious question, then, is whether the universe is actually Euclidean or hyperbolic. Note that it is not possible to "prove" that the world is Euclidean by measuring a physical triangle and showing that it has 180 degrees. Why? However, if the universe were hyperbolic, it might be possible to show this by measuring triangles. How? In fact, the great mathematician Gauss tried to do exactly this!

The course rewards careful, attentive reading and regular review of previously covered material. Be sure to read with a pencil in your hand, especially to draw figures that relate to the material being discussed.



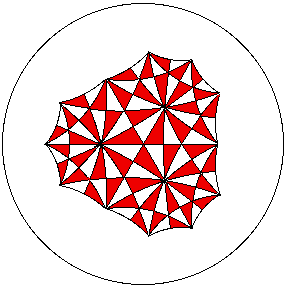
A tiling of the hyperbolic plane by congruent triangles.

Outline of Weekly Readings

Assessment

There will be two take-home exams, one just after mid-term (the week of October 16) and the other will be due on the at the time scheduled for the final exam for this course (Wednesday, 13 December 2000 at 8:30 am). As well, there is a required project for the course (see notes below). It will be due on December 6. I will ask you to present the key ideas from your project to the class during the last week of the term.

The take-home final will cover material primarily from the second half of the course and will include a careful review of hyperbolic geometry that will require a number of hyperbolic constructions. (E.g., construct an equilateral triangle with three 45 degree angles!)

Assignments are due at the beginning of class. Late assignments will incur a substantial penalty and will be rejected entirely if more than two days late. Since the course builds on each assignment, it is extremely important for you to get them done on time.

I encourage you to discuss material with each other. However, each person should write up her or his work individually. On the take-home exams you should not even discuss the problems with your classmates.

Together the take-home mid-term and final assignments count for 45\% of your final grade. The project counts for 15\%. Homework assignments will make up the remainder (40\%) of your grade, though I reserve the right to consider class participation as a factor.

Office Hours

My office is located in Lansing 305. My extension is 3619. I have scheduled office hours on MW 2:30--3:30, TT 12:30--1:30. I am often in my office at other times of the day, and I encourage you to drop in to get hints or help with course assignments or just to chat.

Project Guidelines

Your project for the course is due Monday, 4 December 2000 (the beginning of the last week of classes). Your project should be the equivalent of 7--10 pages typewritten. Feel free to submit a handwritten copy if your writing is very neat and legible. Your topic should be approved in advance. I will ask for a project proposal and outline on Friday, 29 October 2000 if you have not already submitted one.

The following are possible topics that come from our text. Some are essays or "research papers" while others consist of one of more "Major Exercises." Other topics are possible, but please seek approval prior to 29 October 2000.

Additional Sources on Reserve

The following texts have been placed On Reserve in the Library. Readings will be assigned in some of these texts, others are for your reference.

This document last updated on 24 August 2000. Send comments to: mitchell@hws.edu.