Michael Markzon

19 November 1996

Various species of Acropora were examined at the reef flats of Lady Elliot Island on the Great Barrier Reef to determine if their branching patterns were similar. Acropora are known to have properties which enable them to grow in a c oordinated fashion. It was found that the bifurcation ratios of the corals observed fit a normal distribution. In addition, it was found that the Tributary to Source ratios for both Primary and Secondary branches fit a normal distribution. The preliminary results from this study can be used to find the significance of other factors that affect coral growth.

Acropora, from the family Acroporidae, is a genus of stony branching coral which is commonly referred to as staghorn coral. It is common in shallow water, including exposed upper reef slopes and reef flats, and is successful because its species have light skeletons which allow them to grow quickly and overcome their neighbors. Acropora distinguishes itself by its method of branching. As its central axial polyp increases in length it buds off smaller radial polyps from its sides (Wallace 1979). Because of these specialized axial polyps, the corallites of a colony are closely interconnected and can grow in a coordinated fashion. While the corallite branches appear to be growing randomly, a question that must be asked is whether these branches are in fact forming a random pattern. Measures first designed to describe streaming networks (Horton, 1932, 1945; Strahler 1952) have later been used to describe branching corals (Brazeau and Lasker 1988; Mitchell et al. 1992). This pape r will use the system developed by Horton and adapted by Strahler, to examine the patterns in Acropora, and determine if branching occurs randomly.

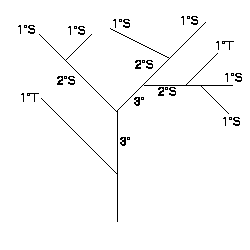
The branching patterns of the coral were classified according to a system first developed by Horton (1932, 1945) and modified by Strahler (1952). McMahon and Kronauer (1976) explained how the method worked. The most distal branches were assig ned order number 1 (1°). When two first-order branches joined, they formed a branch of order 2 (2°). When a branch of lower order met a branch of higher order, the resulting branch retained the order of the higher ordered branch. For example, if a 2° m erged with a 3°, the resulting branch was of order 3°. Thus, higher order branches arose only when two branches of lower order joined. Figure 1 diagrams this system.

To compare branching systems of different samples, a bifurcation ratio (R_b) was determined. This was the ratio of the number of branches of a given order to the number of branches of the next higher order. The R_b for a branc hing network was found by first plotting the log of the number branches versus the order of the branch. Then the slope of the regression line was found, and the antilog of the absolute value of the slope was determined. This was the bifurcation ratio.

Figure 1: Branching structure showing first, second and third order branches and tributary (T) and source (S) branches. For this branch R_b=2.8, 1°T/S=0.33, 2°T/S=0.50 (Brazeau and Lasker 1988).

Another ordering system that was used distinguished between branches which did not increase the order, and those which did increase the order of the system (Mock 1971). Sources were those branches which joined others of the same order to form a branch of a higher order. Branches of lower order which joined branches of higher order were called tributary sources. A tributary to source ratio (T/S) was then found.

Ten colonies of Acropora were observed in the reef flats at Lady Elliot Island on the Great Barrier Reef, Queensland, Australia. Because the coral could not be removed from its source it was difficult to see many "whole" pieces of cor al. Therefore, the majority of the pieces that were used for data collection came from the outside edge of the colonies. Branch order and type were recorded.

Table 1 shows the ratio of tributary to source branches and the bifurcation ratios of the ten samples of Acropora examined.

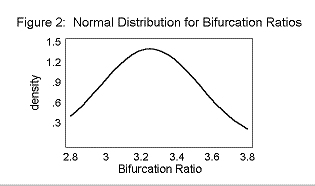
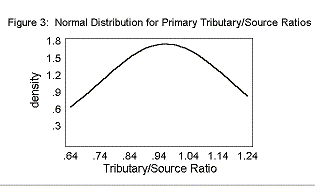
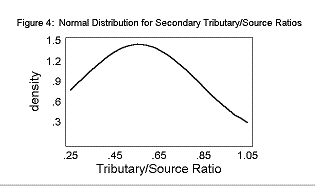
The mean Primary T/S was 0.96± 0.23. The mean Secondary T/S was 0.56± 0.28. The mean R_b was 3.25± 0.28.

The T/S ratios and the Bifurcation Ratios fit a normal distribution curve, as shown in Figures 2, 3, and 4.

The results show that while the colonies of Acropora appeared to follow the same pattern of branching, they do not all have the same bifurcation ratios. This difference is only statistical, however, and can not be noticed when one is lookin g at Acropora, as the branches appear to be interconnected almost as if they were of the same individual (personal observation).

The tributary to source ratios for both primary and secondary branches also differed among their respective sample sets. This difference could be noticed while the data was being collected. Often times, for example, there would be branches with m any tributary branches at the top of the main branch, while at other times, there would be branches with no additional tributary branches. From a personal observation, this difference appeared to be random.

Branching systems of corals can effect other aspects of both the coral and the organisms which surround it. These include how light reaches the coral, how the coral obtains food, and how other organisms relate with the coral. Wallace (1979, p. 12 ) pointed out that the best documented shape alteration for Acropora to receive light occurred as it flattened out horizontally with an increased water depth. This allowed the polyps to position themselves efficiently in response to decreased ligh t intensity.

This change in positioning is also common in another type of branching coral, Scleractinia (Sebens and Johnson 1991). It was found that Scleractinian coral species that existed in low light conditions produced flat plating colonies which maximized lig ht captured from directly above.

Specialized branches can also help Acropora obtain food. It is known that higher water flow speeds lead to higher growth rates (Sebens 1991). Because corals depend on water movement to deliver prey to their tentacles, it is proposed that Ac ropora’s branching patterns have adapted to allow water to flow through them at a maximum rate. In addition, according to Wallace, there is a consensus that for corals, space becomes a premium before food. It is again proposed that Acropora has adjusted to this by having a light skeleton which allows it to grow quickly and fill a large area. If growth can occur quickly, then more energy is left for the intake of food.

Acropora is also a popular habitat for other marine species, including shrimp, crabs, and fishes (Patton 1994). These groups of fauna inhabit the spaces between the branches of the coral. The way the branches of Acropora have grown has affected the way other species have evolved. Species have adapted so that they can monopolize the coral resource. Closely branched colonies of Acropora typically contain more animals than more open corals.

The coral branches also provide protection from predation, and at the same time assist in the mating patterns of certain organisms (Patton 1994). A host animal can release target chemicals that allow another of the same type of individual to find it i n the coral. Those that respond to the host chemicals will be able to find a mate easily, without spending dangerous search time on their own.

Further study in the area of Acropora branching should incorporate different species of the coral. In this way, tests such as ANOVA’s can be carried out to determine relationships between the species. In addition, more coral specific tests can be carried out that relate other aspects discussed here, such as types of inhabitants, light availability and coral size, and adaptations for feeding. Since it is now known that the bifurcation ratios, and T/S ratios fit normal distributions, T-tests, a s well as other tests that rely on a normal distribution, can be used when necessary.

Brazeau, DA, Lasker, HA (1988) Inter- and intraspecific variation in gorgonian colony morphology: quantifying branching patterns in arborescent animals. Coral Reefs 7:139-143.

Horton RE (1932) Drainage basin characteristics. Eos Trans An Geophys Union 13:350-361.

Horton RE (1945) Erosional development of streams and their drainage basin; hydrophysical approach to quantitative morphology. Geological Society of America Bulletin 56:275-370.

McMahon TA, Kronauer RE (1976) Tree structures: deducing the principle of mechanical design. Journal of Theoretical Biology 59:443-466.

Mitchell ND, Dardeau MR, and Schroeder WW (1993) Colony morphology, age structure, and relative growth of two gorgonian corals, Leptogorgia hebes (Verrill) and Leptogorgia virgulata (Lamarck), from the northern Gulf of Mexico. Coral R eefs 12:65-70.

Mock SJ (1971) A classification of channel links in stream networks. Water Resource Research 7:1558-1566.  

Patton WK (1994) Distribution and ecology of animals associated with branching corals (Acropora spp.) from the Great Barrier Reef, Australia. Bulletin of Marine Science 55(1):193-211.

Sebens KP (1991) Effects of water-flow on coral growth and prey capture. American Zoology 31(5):59a (abstract only).

Sebens KP, Johnson AS (1991) Effects of water movement on prey capture and distribution of reef corals. Hydrobiologia 226:91-101.

Strahler AN (1952) Hypsometric (area-altitude) analysis of erosional topography. Geological Society of America Bulletin 64:165-176.

Vernon JEN (1986) Corals of Australia and the Indo-Pacific. Angus and Robertson Publishers: North Byde, NSW.

Wallace, CC (1979) Patterns within assemblages of the coral genus Acropora on the Great Barrier Reef, Queensland. Ph.D. Thesis, University of Queensland.